La parabola è il luogo geometrico dei punti equidistanti da una retta (direttrice) e da un punto (fuoco).
La parabola è il luogo geometrico dei punti equidistanti da una retta (direttrice) e da un punto (fuoco).
La retta passante per il fuoco e perpendicolare alla direttrice si chiama asse della parabola.
L'asse della parabola è un asse di simmetria e interseca la parabola nel vertice.
Una parabola con asse parallelo all'asse y è rappresentata da un'equazione del tipo:
y = ax2 + bx + c (con a diverso da 0)
Nel grafico seguente è rappresentata una parabola generica (con asse parallelo all'asse y), e sono evidenziate le sue caratteristiche fondamentali (si veda la tabella riportata poco più sotto).
FORMULARIO:

Concavità e "apertura" della parabola dipendono dal parametro a (come si nota chiaramente dalle due immagini sottostanti)


CASISTICA:
Equazione di una parabola con asse parallelo all'asse y: y = ax2 + bx + c (con a diverso da 0)
Equazione di una parabola con asse parallelo all'asse x: x = ay2 + by + c (con a diverso da 0)
Equazione di una parabola con Vertice V sull'asse delle y: y = ax2 + c (con b = 0)
Equazione di una parabola passante per l'Origine: y = ax2 + bx (con c = 0)
Equazione di una parabola con Vertice V coincidente con l'Origine: y = ax2 (con b = 0 e c = 0)
ESERCIZIO GUIDATO:
Scrivere l'equazione della parabola con asse parallelo all'asse y che ha vertice in V(1,2) e passa per il punto A(2,1).
Si considera l'equazione generale di una parabola con asse parallelo all'asse y: y = x 2 + bx + c
Si impongono le condizioni date. Si noti che la conoscenza delle coordinate del vertice equivale a due condizioni.

da questo si ricava

sostituendo il valore di b nelle altre due equazioni, si ha:

da cui, infine: a = 1 b = 2 c = 1
Si noti che l'equazione di secondo grado in a, fornisce anche la soluzione a = 0: questa però non è accettabile, dal momento che l'equazione generale di una parabola non rappresenta una parabola se a = 0.
Pertanto, la parabola cercata ha equazione: y = - x2 + 2x + 1
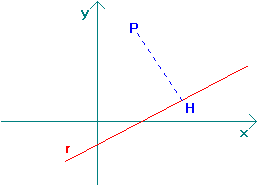 Sia P ( x0 , y0 ) e sia r la retta di equazione implicita ax + by + c = 0.
Sia P ( x0 , y0 ) e sia r la retta di equazione implicita ax + by + c = 0. ![]()
![]()