![]() Sono tutti quei solidi ottenuti dalla rotazione di una figura piana intorno ad una retta (asse di rotazione).
Sono tutti quei solidi ottenuti dalla rotazione di una figura piana intorno ad una retta (asse di rotazione).
CILINDRO:
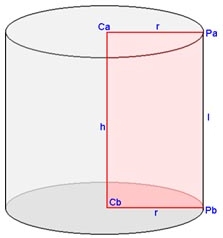 Il cilindro è un solido ottenuto dalla rotazione completa di un rettangolo intorno ad un suo lato.
Il cilindro è un solido ottenuto dalla rotazione completa di un rettangolo intorno ad un suo lato.
Cilindro equilatero: È un cilindro in cui l’altezza è lunga quanto il diametro della base.
L’area della superficie base di un cilindro si ottiene facendo: AB = πr2
L’area della superficie laterale di un cilindro si ottiene moltiplicando la lunghezza della circonferenza di base per la misura dell’altezza: AL = 2πr · h
L’area della superficie totale di un cilindro si ottiene sommando la superficie laterale e l’area delle due basi: AT = AL + 2AB
Il volume di un cilindro si ottiene moltiplicando l’area di base per la misura dell’altezza: V = AB · h = πr2 · h
CONO:
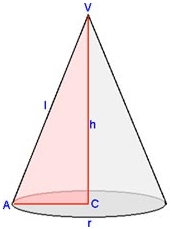 Il cono è un solido ottenuto dalla rotazione di un triangolo intorno ad un suo cateto.
Il cono è un solido ottenuto dalla rotazione di un triangolo intorno ad un suo cateto.
Cono equilatero: È un cono in cui l’apotema è lungo quanto il diametro della base.
L’area della superficie base di un cilindro si ottiene facendo: AB = πr2
L’area della superficie laterale di un cono si ottiene moltiplicando la lunghezza della circonferenza di base per la misura dell’apotema (a, nella figura = l) e dividendo tale prodotto per due: AL = 2πr · a
L’area della superficie totale di un cono si ottiene sommando la superficie laterale e l’area della base: AT = AL + AB
Proprietà. Il cono è equivalente a un terzo di un cilindro avente base ed altezza congruenti rispettivamente alla base e all’altezza del cono.
Il volume di un cono si ottiene moltiplicando l’area di base per la misura dell’altezza e dividendo tale prodotto per tre: V = (AB · h)/3 = (πr2 · h)/3
SFERA:
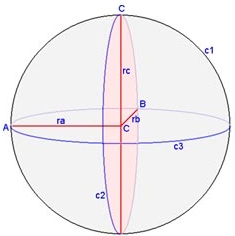 La sfera è un solido ottenuto dalla rotazione completa di un semicerchio attorno al proprio diametro, il raggio e il centro del semicerchio sono il raggio e il centro della sfera.
La sfera è un solido ottenuto dalla rotazione completa di un semicerchio attorno al proprio diametro, il raggio e il centro del semicerchio sono il raggio e il centro della sfera.
La superficie sferica è l’insieme di tutti e solo i punti dello spazio che hanno la stessa distanza da un punto interno detto centro.
Proprietà. La superficie sferica è equivalente alla superficie laterale del cilindro equilatero circoscritto ad essa.
L’area della superficie sferica si ottiene moltiplicando per quattro l’area del suo cerchio massimo: A = 4πr2
Proprietà. Una sfera è equivalente a un cono avente per altezza il raggio della sfera e per raggio di base il diametro della sfera.
Il volume della sfera si ottiene moltiplicando per il cubo del suo raggio: V = 4/3 πr3
TRONCO DI CONO:
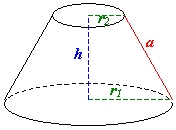 Consideriamo un cono e tagliamolo con un piano parallelo al piano della base: otteniamo due figure, una è ancora un cono, l’altra è un tronco di cono.
Consideriamo un cono e tagliamolo con un piano parallelo al piano della base: otteniamo due figure, una è ancora un cono, l’altra è un tronco di cono.
Il tronco di cono è un solido attenuto dalla rotazione di un trapezio rettangolo attorno al lato perpendicolare alle basi.
Proprietà. La superficie laterale di un tronco di cono è equivalente a un trapezio avente per basi le due circonferenze di base del tronco e per altezza il suo apotema.
L’area della superficie laterale di un tronco di cono si ottiene moltiplicando la somma delle misure delle lunghezze delle due circonferenze di base per la misura dell’apotema e dividendo tale prodotto per due: AL = π(r1 + r2) · a
L’area della superficie totale di un cono si ottiene sommando la superficie laterale e l’area delle due basi: AT = AL + AB1 + AB2
Proprietà. Per il principio di Cavalieri, un tronco di cono e un tronco di piramide aventi basi equivalenti e altezze congruenti sono equivalenti.
Il volume di un cono si ottiene moltiplicando la misura dell’altezza per la somma dell'area di base con l'area del tronco e con la radice quadrata del loro prodotto, e dividendo tale prodotto per tre: [(AB1 + AB2) + SQRTAB1 + AB2]· h/3
