POTENZE CON ESPONENTE NATURALE:

Possiamo moltiplicare 5 per tre volte con se stesso, cioè formare il prodotto 5 × 5 × 5 e indicarlo con 5³.
Possiamo farlo con  qualsiasi numero (reale) e usare simboli astratti: Se a è un numero, la notazione a³ sta a indicare a × a × a, e se vogliamo lasciare in sospeso anche il numero dei fattori, scriviamo aⁿ ( "a alla n"), dove n rappresenta un numero naturale qualsiasi (n = 1, 2, 3,...) . Chiamiamo

• aⁿ una potenza (la "potenza n-esima di a"; si dice anche: "a elevato alla n")
  
• a la base
  
• n l' esponente.

PROPRIETA' DELLE POTENZE:

• Prodotto di potenze di uguale base                aⁿa^m=a^n+m
  es. 2³·2³ = 2³⁺³= 2⁶
  
• Quoziente di potenze di uguale base              aⁿ: a^m=a^n-m
  es. 2⁶·2³ = 2^6-3 = 2³
• Potenza di una potenza                                 (aⁿ)^m=a^nm
  es. (2³)² = 2^2·3 = 2⁶
  
• Prodotto di potenze con uguale esponente        aⁿbⁿ=(ab)ⁿ
  es. 2⁴·5⁴ = (2·5)⁴ = 10⁴
• Quoziente di potenze con uguale esponente      aⁿ: bⁿ=(a:b)ⁿ
  es. 10⁴/5⁴ = (10/5)⁴ = 2⁴

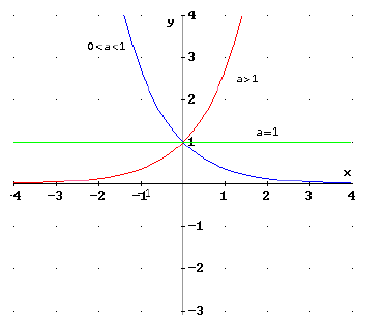
STUDIO DELLA FUNZIONE:

La funzione y = a^x viene separata in tre casi

• CASO 1 (Verde): a = 1 --> qualsiasi sia la potenza di 1 otteniamo 1. (è una retta parallela all'asse delle x passante per il punto P (0;1) FUNZIONE COSTANTE
  
  
• CASO 2 (Rosso): a > 1 --> I valori di y crescono al crescere di x, passa per il punto P (0;1) FUNZIONE CRESCENTE
  
  
• CASO 3 (Blu): 0 < a < 1 --> I valori di y diminuiscono al crescere di x, passa per il punto P (0;1) FUNZIONE DECRESCENTE

Si nota bene che non esisterà mai un valore della y minore di 0.