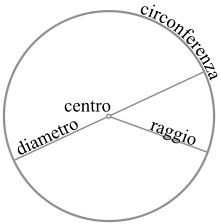
In geometria, il cerchio è la parte delimitata da una circonferenza, ovvero l'insieme dei punti che distano da un punto dato detto centro non più di una distanza fissata detta raggio

Area Cerchio: A = π·Raggio² [cm²]

Lunghezza Circonferenza: C = 2·π·Raggio [cm]

PROPRIETA' PARTICOLARI:

• Ogni triangolo rettangolo è inscrivibile in un semicerchio.
• In ogni triangolo rettangolo, l'ipotenusa coincide con un diametro del cerchio circoscritto.

FORMULE INVERSE:

Raggio = R = C/2π oppure √(A/π) oppure D/2

ESEMPIO:

Data un circonferenza di raggio pari a 5 cm calcolare area e perimetro.

Area = A = π·R² = π·5² = 3,14·25 = 78,5 cm²

Circonferenza = C = 2·π·R = 2·3,14·5 = 31,4 cm

Diametro = D = 2· R = 2 ·5 = 10 cm

Equazione della circonferenza passante per tre punti non allineati:

Per determinare l'equazione della circonferenza passante per tre punti P1(x1,y1) ,P2(x2,y2), P3(x3,y3) occorre imporre la condizione di appartenenza di ciascun punto alla curva ottenendo in tal modo un sistema di tre equazioni nelle tre incognite a, b, c.

Se i punti non sono allineati il sistema è determinato ed ammette  una sola soluzione.

ESERCIZIO GUIDATO:

Determinare l'equazione della circonferenza passante per i tre punti A(-1,-4), B(0,3), C(7,2)

SOLUZIONE:

Imposto il sistema di riferimento e calcolo i valori di a, b, c.

L'equazione della circonferenza risulta quindi: x² + y² -15x -6y +2 = 0